Essential length of roller chain
Employing the center distance between the sprocket shafts plus the number of teeth of the two sprockets, the chain length (pitch variety) could be obtained through the following formula:
Lp＝（N1 ＋ N2）/2＋ 2Cp＋｛（ N2－N1 ）／2π｝2
Lp : Overall length of chain (Pitch variety)
N1 : Quantity of teeth of little sprocket
N2 : Variety of teeth of large sprocket
Cp: Center distance amongst two sprocket shafts (Chain pitch)
The Lp (pitch quantity) obtained in the over formula hardly gets an integer, and generally involves a decimal fraction. Round up the decimal to an integer. Use an offset hyperlink in case the number is odd, but decide on an even quantity around possible.
When Lp is established, re-calculate the center distance amongst the driving shaft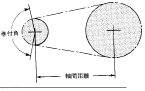 
and driven shaft as described from the following paragraph. In case the sprocket center distance can't be altered, tighten the chain making use of an idler or chain tightener .
Center distance among driving and driven shafts
Certainly, the center distance among the driving and driven shafts needs to be more than the sum with the radius of both sprockets, but usually, a correct sprocket center distance is deemed to become 30 to 50 instances the chain pitch. However, should the load is pulsating, twenty times or less is right. The take-up angle in between the little sprocket along with the chain have to be 120°or much more. In the event the roller chain length Lp is provided, the center distance concerning the sprockets could be obtained from your following formula:
Cp＝１/4Lp－(N1＋N2)/2+√(Lp－(N1＋N2)/2)^2－2/π2（N2－N1）^2
Cp : Sprocket center distance (pitch quantity)
Lp : Total length of chain (pitch quantity)
N1 : Amount of teeth of little sprocket
N2 : Variety of teeth of big sprocket
